0. Introduction (4 pts)

COVID-19 has emerged at a unique time in our history in which even public health has become politicized. I chose to study the correlation between mask usage and COVID-19 outcomes in an attempt to understand how reduced mask use impacts the number of COVID-19 cases and deaths per U.S. county. The COVID-19 data was collected by the New York Times and includes the total number of cases and deaths as of October 4. The mask frequency survey was also published by the New York Times and was collected through online interviews by the survey firm Dynata in the month of July. Lastly, the population data was published by the U.S. Census Bureau and includes 2019 population estimates per county.

I expect population size to strongly correlate with the number of COVID-19 cases and deaths. I also predict that counties that have reported higher frequencies in mask use will have better health outcomes during this pandemic, with less people contracting the virus and, as a result, less fatalities.

1. Tidying: Rearranging Wide/Long (8 pts)

mask_usage %>% pivot_longer(2:6, names_to = "mask_use", values_to = "frequency")

## # A tibble: 15,710 x 3
##    COUNTYFP mask_use   frequency
##    <chr>    <chr>          <dbl>
##  1 01001    NEVER          0.053
##  2 01001    RARELY         0.074
##  3 01001    SOMETIMES      0.134
##  4 01001    FREQUENTLY     0.295
##  5 01001    ALWAYS         0.444
##  6 01003    NEVER          0.083
##  7 01003    RARELY         0.059
##  8 01003    SOMETIMES      0.098
##  9 01003    FREQUENTLY     0.323
## 10 01003    ALWAYS         0.436
## # … with 15,700 more rows

mask_usage %>% pivot_longer(2:6, names_to = "mask_use", values_to = "frequency") %>% 
    pivot_wider(names_from = "mask_use", values_from = "frequency")

## # A tibble: 3,142 x 6
##    COUNTYFP NEVER RARELY SOMETIMES FREQUENTLY ALWAYS
##    <chr>    <dbl>  <dbl>     <dbl>      <dbl>  <dbl>
##  1 01001    0.053  0.074     0.134      0.295  0.444
##  2 01003    0.083  0.059     0.098      0.323  0.436
##  3 01005    0.067  0.121     0.12       0.201  0.491
##  4 01007    0.02   0.034     0.096      0.278  0.572
##  5 01009    0.053  0.114     0.18       0.194  0.459
##  6 01011    0.031  0.04      0.144      0.286  0.5  
##  7 01013    0.102  0.053     0.257      0.137  0.451
##  8 01015    0.152  0.108     0.13       0.167  0.442
##  9 01017    0.117  0.037     0.15       0.136  0.56 
## 10 01019    0.135  0.027     0.161      0.158  0.52 
## # … with 3,132 more rows

The data from all three sets is already tidy, with every variable having a distinct column. However, as shown above, when I pivot the mask use dataset longer, the mask frequency categories (rarely, sometimes, frequently and always) are put into one big column. Their values are then put into a separate column. However, this makes the data harder to analyze and much, much longer. Therefore, I pivoted the mask use dataset wider again, returning it to its original tidy format.

2. Joining/Merging (8 pts)

population_est <- population_est %>% as.data.frame() %>% mutate(county = str_replace(county, 
    ".", "")) %>% mutate(county = str_replace(county, "County", 
    "")) %>% separate(county, into = c("county", "state"), sep = " , ") %>% 
    unite(county, state, col = "location")

# Joining the COVID data
covid_data_partial <- us_counties %>% full_join(mask_usage, by = c(fips = "COUNTYFP")) %>% 
    select(-1) %>% unite(county, state, col = "location")

# Joining the full dataset
covid_data_full <- covid_data_partial %>% full_join(population_est, 
    by = "location") %>% select(-(5:8))

First, I had to alter the "county" variable in the population dataset (population_est) so that I could combine the three datasets by location. I combined county and state information into one variable simply because multiple states have counties with the same name. I then combined the county COVID-19 dataset (us_counties) with the mask frequency survey (mask_usage) using a full join in order to preserve the original data.

3. Wrangling (40 pts)

covid_data_full <- covid_data_full %>% mutate(score = 1 * NEVER + 
    2 * RARELY + 3 * SOMETIMES + 4 * FREQUENTLY + 5 * ALWAYS) %>% 
    select(-c("NEVER", "RARELY", "SOMETIMES", "FREQUENTLY", "ALWAYS")) %>% 
    separate(location, into = c("county", "state"), sep = "_") %>% 
    select(-fips) %>% mutate(case_fatality_ratio = ((deaths)/(cases)))

state_covid <- covid_data_full %>% group_by(state) %>% summarize(avg_score = mean(score), 
    sd_score = sd(score), est_pop = sum(est_pop), cases = (sum(cases)), 
    deaths = (sum(deaths)), case_fatality_ratio = (sum(deaths)/sum(cases)))
glimpse(state_covid)

## Rows: 56
## Columns: 7
## $ state               <chr> "Alabama", "Alaska", "Arizona", "Arkansas", "Cali…
## $ avg_score           <dbl> 3.921522, NA, 4.304400, NA, 4.492431, 4.189328, N…
## $ sd_score            <dbl> 0.2415388, NA, 0.2565571, NA, 0.2152504, 0.332368…
## $ est_pop             <dbl> 4903185, NA, 7278717, NA, 39512223, 5758736, NA, …
## $ cases               <dbl> 158380, 9111, 220403, 86525, 831494, 72929, 58297…
## $ deaths              <dbl> 2558, 54, 5705, 1407, 16122, 2071, 4513, 645, 629…
## $ case_fatality_ratio <dbl> 0.016151029, 0.005926902, 0.025884403, 0.01626119…

state_covid %>% summarize(`Correlation Between Mask Use and Case Fatality Ratio` = cor(avg_score, 
    case_fatality_ratio))

## # A tibble: 1 x 1
##   `Correlation Between Mask Use and Case Fatality Ratio`
##                                                    <dbl>
## 1                                                     NA

state_covid %>% arrange(-est_pop)

## # A tibble: 56 x 7
##    state          avg_score sd_score  est_pop  cases deaths case_fatality_ratio
##    <chr>              <dbl>    <dbl>    <dbl>  <dbl>  <dbl>               <dbl>
##  1 California          4.49    0.215 39512223 831494  16122              0.0194
##  2 Texas              NA      NA     28995881     NA     NA             NA     
##  3 Pennsylvania        4.41    0.235 12801989 166270   8271              0.0497
##  4 Ohio                3.81    0.297 11689100 157966   4925              0.0312
##  5 North Carolina      4.25    0.226 10488084 217049   3647              0.0168
##  6 Arizona             4.30    0.257  7278717 220403   5705              0.0259
##  7 Indiana             3.87    0.242  6732219 126414   3669              0.0290
##  8 Colorado            4.19    0.332  5758736  72929   2071              0.0284
##  9 South Carolina      3.99    0.251  5148714 150891   3442              0.0228
## 10 Alabama             3.92    0.242  4903185 158380   2558              0.0162
## # … with 46 more rows

covid_data_full %>% group_by(state) %>% summarize(avg_score = mean(score), 
    sd_score = sd(score), est_pop = sum(est_pop), cases_per_capita = (sum(cases)/1e+05), 
    deaths_per_capita = (sum(deaths)/1e+05)) %>% glimpse

## Rows: 56
## Columns: 6
## $ state             <chr> "Alabama", "Alaska", "Arizona", "Arkansas", "Califo…
## $ avg_score         <dbl> 3.921522, NA, 4.304400, NA, 4.492431, 4.189328, NA,…
## $ sd_score          <dbl> 0.2415388, NA, 0.2565571, NA, 0.2152504, 0.3323681,…
## $ est_pop           <dbl> 4903185, NA, 7278717, NA, 39512223, 5758736, NA, NA…
## $ cases_per_capita  <dbl> 1.58380, 0.09111, 2.20403, 0.86525, 8.31494, 0.7292…
## $ deaths_per_capita <dbl> 0.02558, 0.00054, 0.05705, 0.01407, 0.16122, 0.0207…

texas_covid <- covid_data_full %>% filter(state == "Texas") %>% 
    arrange(-score)
glimpse(texas_covid)

## Rows: 254
## Columns: 7
## $ county              <chr> "Hays", "El Paso", "Hudspeth", "Atascosa", "Presi…
## $ state               <chr> "Texas", "Texas", "Texas", "Texas", "Texas", "Tex…
## $ cases               <dbl> 5951, 25206, 62, 1166, 97, 1063, 29750, 1501, 996…
## $ deaths              <dbl> 66, 531, 3, 32, 7, 18, 429, 77, 40, 0, 35, 1329, …
## $ est_pop             <dbl> 230191, 839238, 4886, 51153, 6704, 20837, 1273954…
## $ score               <dbl> 4.815, 4.805, 4.763, 4.751, 4.746, 4.728, 4.710, …
## $ case_fatality_ratio <dbl> 0.01109057, 0.02106641, 0.04838710, 0.02744425, 0…

First, I converted the mask use frequencies into a "mask use score" where counties with higher scores reported higher frequencies of mask usage. I also found the case fatality ratio in order to analyze the mortality rate among counties. I also grouped by state and found the total number of cases and deaths, as well as the average and standard deviation in mask use score for each state. In addition, I also found the correlation between average mask use scores and case fatality ratios across all of the states. Finally, I filtered the complete data set to make a dataset that only included Texas COVID-19 data and was surprised to see that Hays county has the highest mask use score out of all other Texas counties!

4. Visualizing (30 pts)

ggplot(state_covid, aes(avg_score, cases)) + geom_point(aes(color = est_pop)) + 
    scale_color_gradient(low = "yellow", high = "red") + ggtitle("COVID-19 Cases and Average Mask Use Scores Among U.S. States") + 
    xlab("Average Mask Use Score") + ylab("COVID-19 Cases") + 
    theme_minimal() + scale_x_continuous(lim = c(3, 5))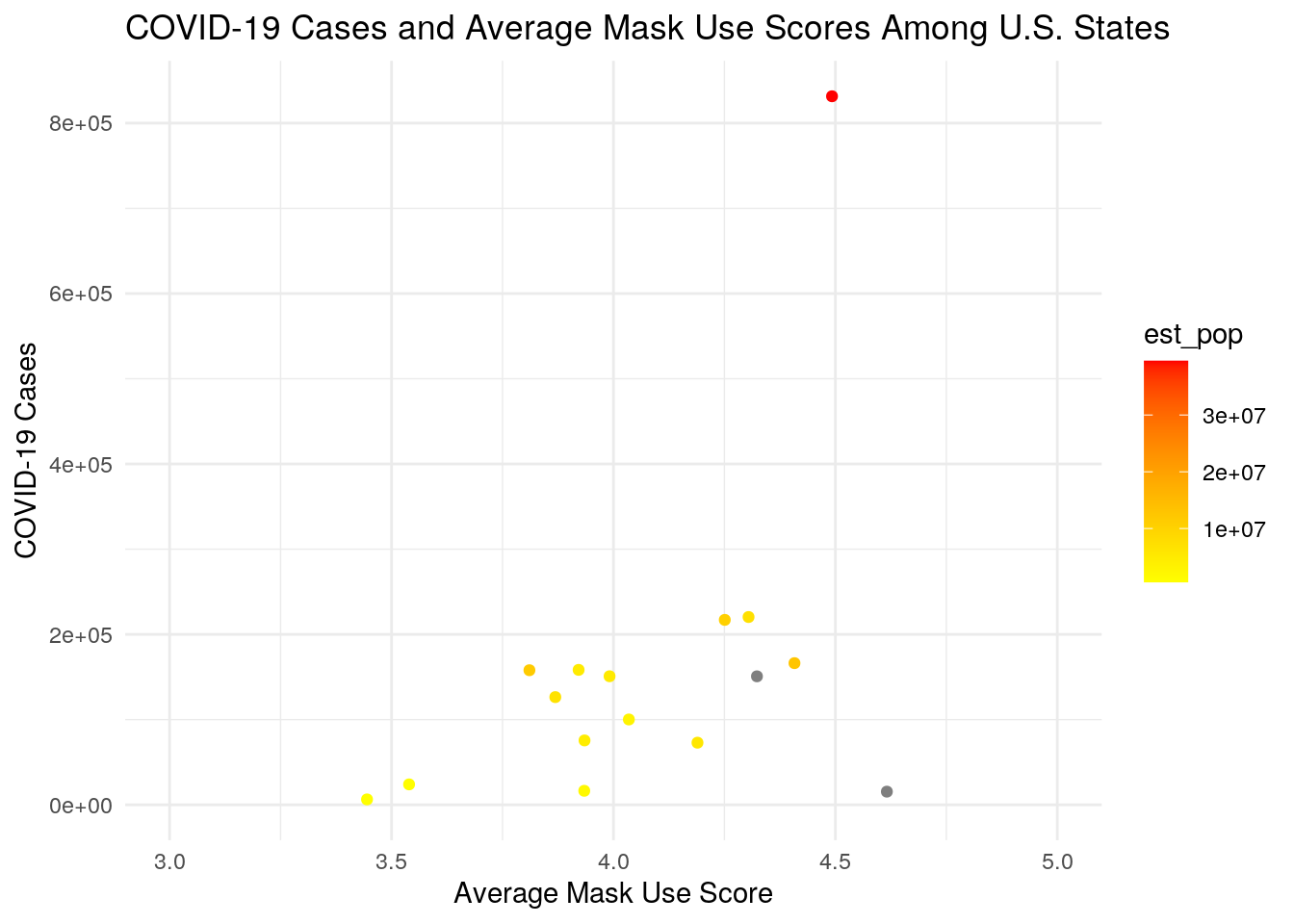

ggplot(state_covid, aes(avg_score, case_fatality_ratio)) + geom_point(aes(color = est_pop)) + 
    scale_color_gradient(low = "grey", high = "purple") + scale_fill_discrete(name = "Estimated\nPopulation") + 
    ggtitle("Percent of Fatal COVID-19 Cases and Average Mask Use Scores\nAmong U.S. States") + 
    xlab("Average Mask Use Score") + ylab("Percent of COVID-19 Cases\nThat Are Fatal") + 
    theme_minimal() + scale_y_continuous(labels = scales::percent)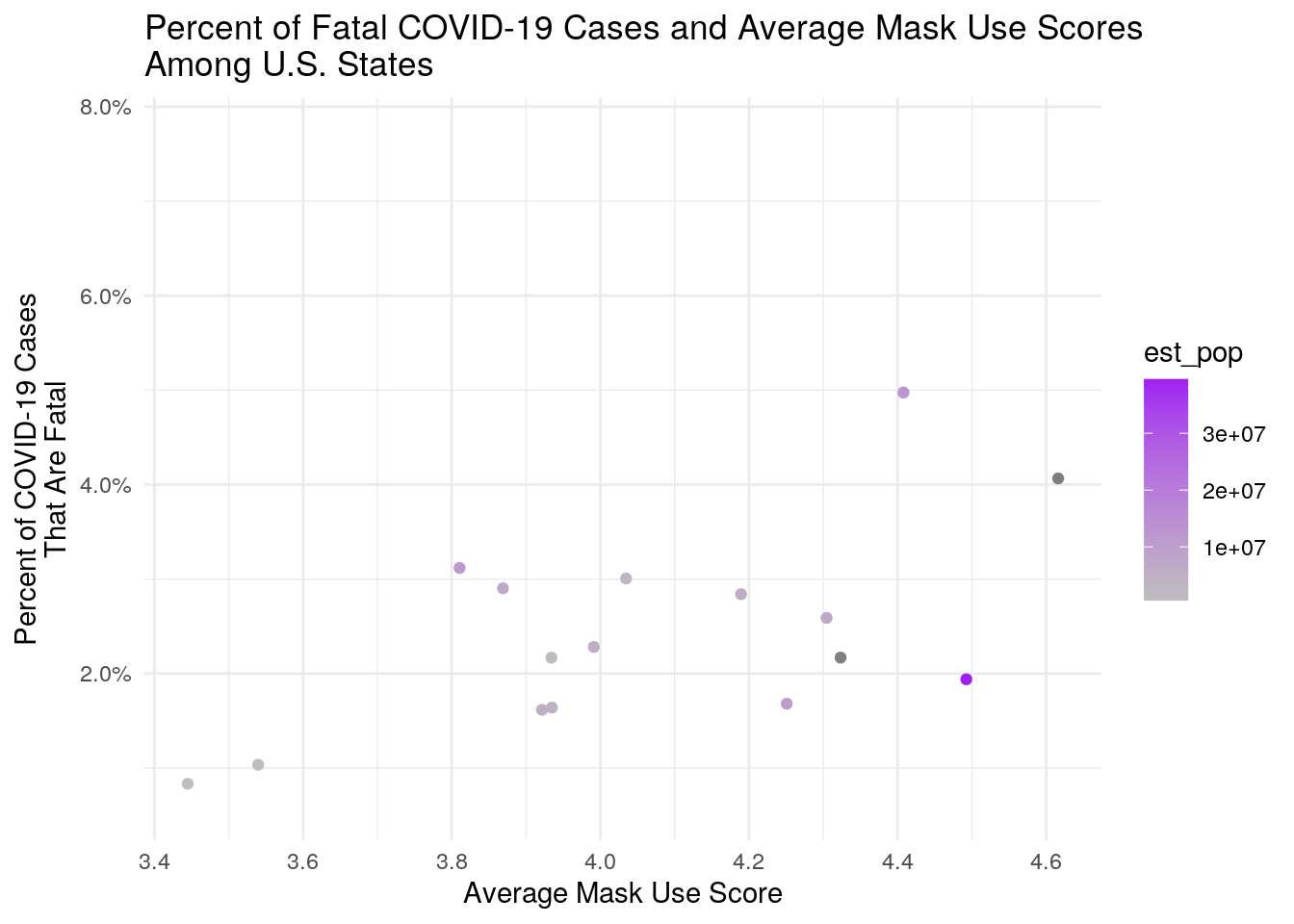

cormat_state <- state_covid %>% select_if(is.numeric) %>% select(-sd_score) %>% 
    cor(use = "pair")

tidycor_state <- cormat_state %>% as.data.frame %>% rownames_to_column("var1") %>% 
    pivot_longer(-1, names_to = "var2", values_to = "correlation")

tidycor_state %>% ggplot(aes(var1, var2, fill = correlation)) + 
    geom_tile() + scale_fill_gradient2(low = "white", high = "red") + 
    geom_text(aes(label = round(correlation, 2)), color = "black", 
        size = 4)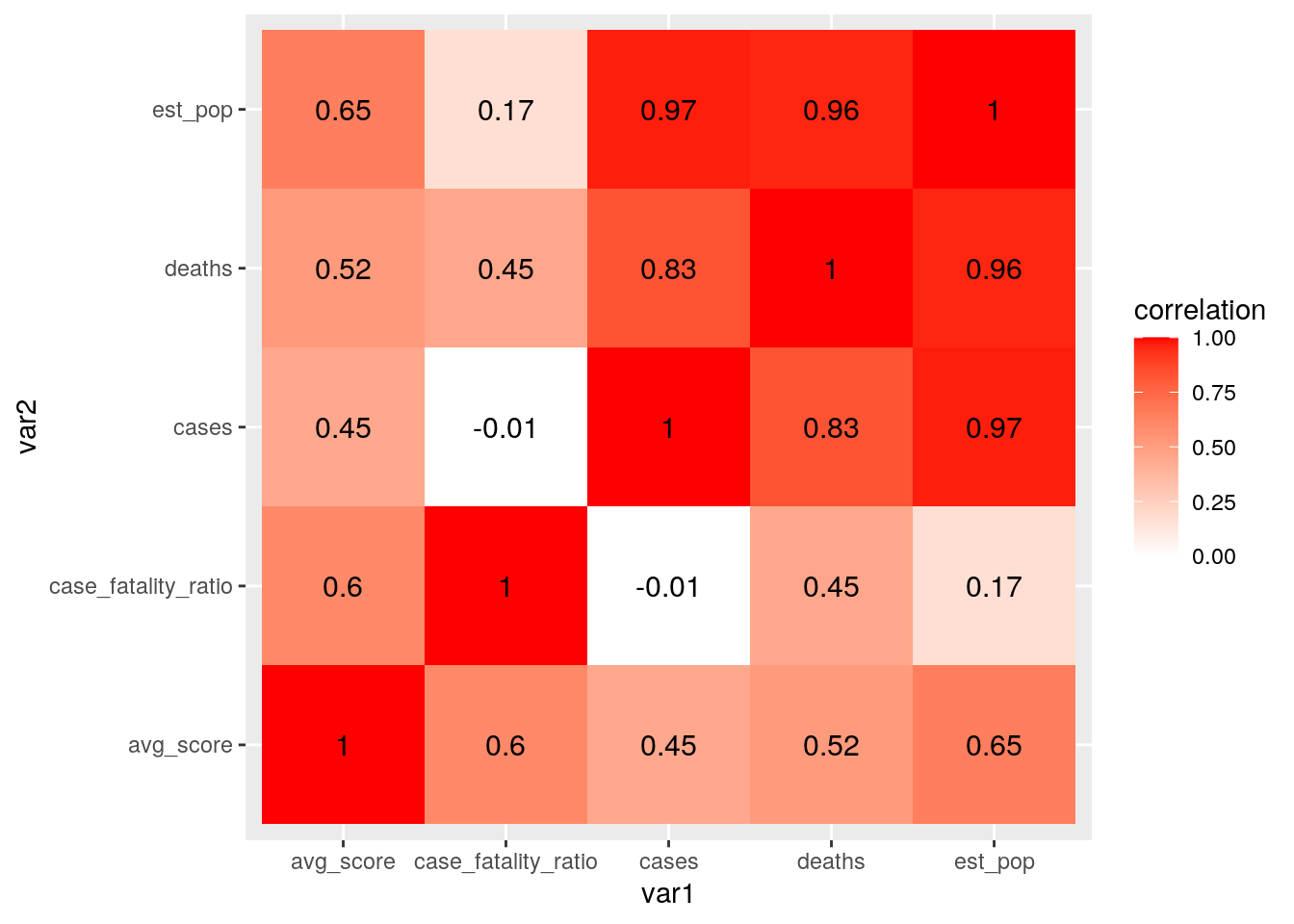

As predicted, there is a strong correlation between population size and COVID-19 cases. There is also a high correlation between population size and COVID-19 deaths. There was also a positive correlation between the case fatality ratio and average mask use score. This could simply be due to the fact that counties experiencing higher mortality rates from COVID-19 are more likely to use masks.

5. Dimensionality Reduction (20 pts)

library(cluster)
library(GGally)
library(plotly)

pam_dat <- state_covid %>% na.omit() %>% select(-state)
sil_width <- vector()
for (i in 2:10) {
    pam_fit <- pam(pam_dat, k = i)
    sil_width[i] <- pam_fit$silinfo$avg.width
}
ggplot() + geom_line(aes(x = 1:10, y = sil_width)) + scale_x_continuous(name = "k", 
    breaks = 1:10)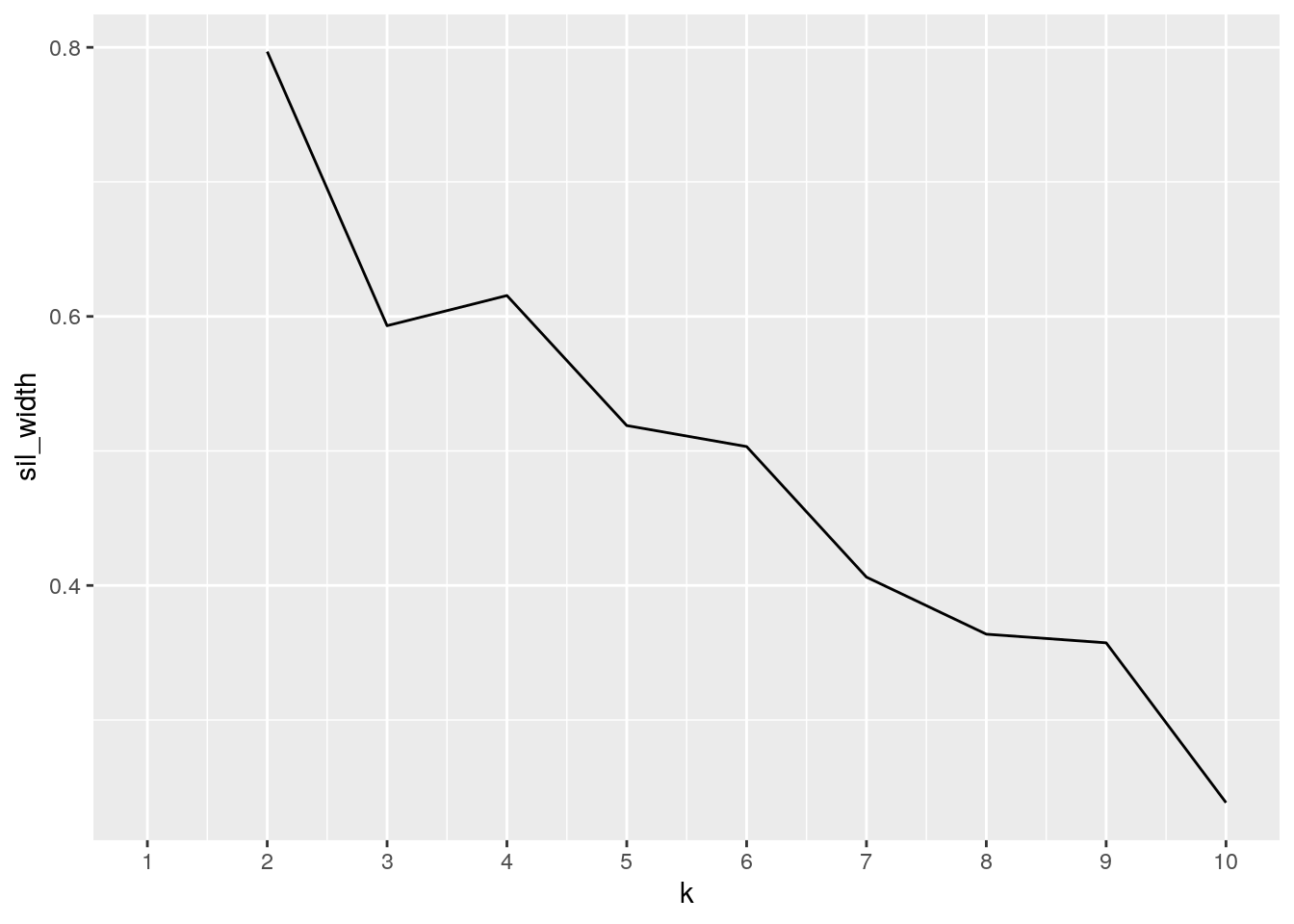

pam1 <- pam_dat %>% pam(k = 5)

pamclust <- pam_dat %>% mutate(cluster = as.factor(pam1$clustering))
pamclust %>% ggplot(aes(x = est_pop, y = cases, color = cluster)) + 
    geom_point() + xlab("Population Size") + ylab("Total COVID-19 Cases")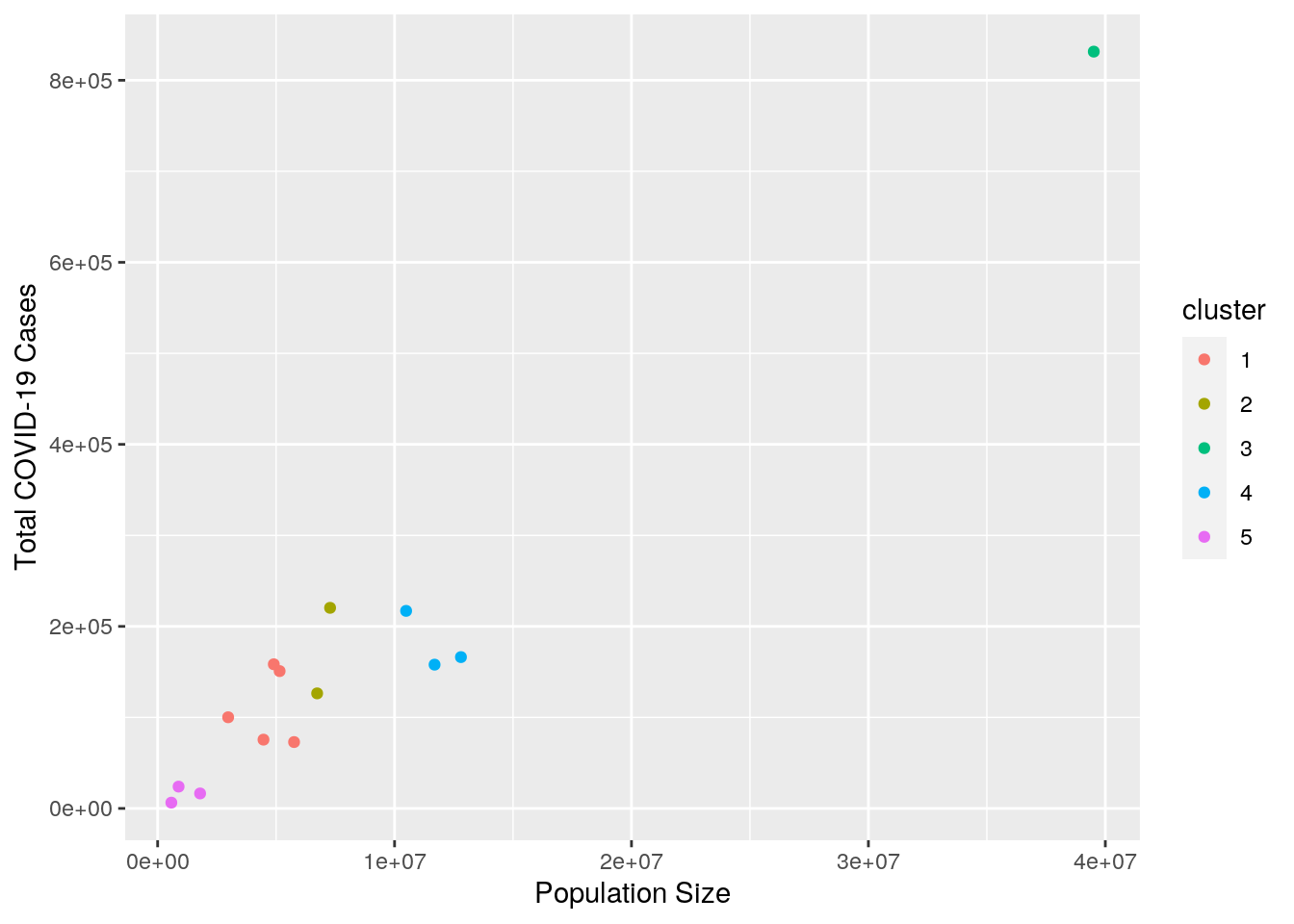

The data forms the clearest clusters when it is grouped in five clusters by total COVID-19 cases and population size. As depicted in the plot above, the amount of cases a state experiences is largely influenced by the size of that population. Therefore, states with similar population sizes tend to have a similar number of cases. California, Texas and Florida, which have population sizes that exceed 20,000,000 and were put into cluster 3, experienced a much higher number of cases compared to states in the other four clusters.

...